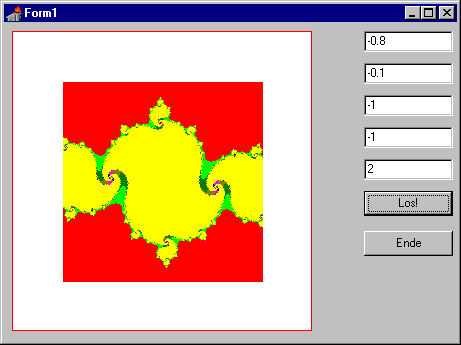

Der französische Mathematiker Gaston Julia hat zu Beginn des 20. Jahrhunderts eine Menge von komplexen Zahlen untersucht. Diese komplexen Zahlen haben die Eigenschaft, dass sie bei der Iteration
z(n+1) = z(n)² + c
konvergieren. Stellt man die komplexen Zahlen, die diese Eigenschaft aufweisen, farblich dar, so erhält man komplizierte Flächenmuster, deren Gestalt von der Wahl der Konstanten c abhängt. Man sich leicht davon überzeugen, dass eine geringfügig anders gewählte Konstante c zu einer deutlich anderen Julia-Menge führt.
Ähnlich wie bei der Mandelbrot-Menge wählen wir ein Quadrat aus der komplexen Zahlenebene aus (Eckpunkt (amin,bmin), Kantenlänge k) und geben eine Konstante c (a,b) aus. Das (im Allgemeinen relativ kleine) Quadrat der komplexen Zahlenebene wird auf einen größeren Bildschirmbereich "gezoomt" (im Beispiel auf 200x200 Pixel). Daraus bestimmen wir die Schrittweite ds:=k/200 für die Iterationen: Wir iterieren für jeden Realteil der komplexen Zahlen im gewählten Quadrat und für jeden Realteil über alle zugehörigen Imaginärteile...
Ist ein Punkt Element der Julia-Menge, wird er (schwarz) eingefärbt.
Strebt ein Punkt der Julia-Menge bei der Iteration gegen Unendlich wird er danach eingefärbt, wie "rasch" er den Kreis mit Radius 2 verlässt - auf diese Weise erscheinen die Punkte in der (näheren) Umgebung der Julia-Menge farbig...
procedure TForm1.Button1Click(Sender: TObject);
var a,b,xmin,ymin,k,ds:real;
x,y,x1,y1,xx:real;
s,z,zaehler:integer;
begin
paintbox1.canvas.pen.color:=clRed;
paintbox1.canvas.brush.color:=clWhite;
paintbox1.canvas.rectangle(0,0,300,300);
a:=StrtoFloat(edit1.text);
b:=StrtoFloat(edit2.text);
xmin:=StrtoFloat(edit3.text);
ymin:=StrtoFloat(edit4.text);
k:=StrtoFloat(edit5.text);
ds:=k/200;
x:=xmin;
for s:=1 to 200 do begin
y:=ymin;
for z:=1 to 200 do begin
x1:=x;
y1:=y;
zaehler:=0;
while (zaehler < 100) and (sqrt(x1*x1+y1*y1)<2) do begin
inc(zaehler);
xx:=x1*x1-y1*y1+a;
y1:=2*x1*y1+b;
x1:=xx;
end;
if (zaehler>=100) then paintbox1.canvas.Pixels[s+50,z+50]:=clYellow;
case zaehler of
0..9:paintbox1.canvas.Pixels[s+50,z+50]:=clRed;
10..19:paintbox1.canvas.Pixels[s+50,z+50]:=clLime;
20..29:paintbox1.canvas.Pixels[s+50,z+50]:=clGreen;
30..39:paintbox1.canvas.Pixels[s+50,z+50]:=clOlive;
40..49:paintbox1.canvas.Pixels[s+50,z+50]:=clFuchsia;
50..59:paintbox1.canvas.Pixels[s+50,z+50]:=clBlack;
60..69:paintbox1.canvas.Pixels[s+50,z+50]:=clPurple;
70..79:paintbox1.canvas.Pixels[s+50,z+50]:=clTeal;
80..89:paintbox1.canvas.Pixels[s+50,z+50]:=clNavy;
90..99:paintbox1.canvas.Pixels[s+50,z+50]:=clAqua;
end;
y:=y+ds;
end;
x:=x+ds;
end;
end;

