Die Ackermann-Funktion

Die Ackermann-Funktion ist für zwei Variable $n$ und $m$ definiert:

$$\begin{eqnarray*} \lefteqn{a(0,m) = m+1} \\ \lefteqn{a(n,0) = a(n-1, 1)} \\ \lefteqn{a(n,m) = a(n-1, a(n, m-1))} \end{eqnarray*}$$

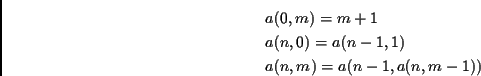
Interessanterweise geht der Rechenaufwand für diese Funktion sehr rasch ``gegen Unendlich''...

public class Ackermann {
    static long ackermann(long n, long m) {
        if (n==0) return m+1;
        else if (m==0) return ackermann(n-1,1);
        else return ackermann(n-1, ackermann(n,m-1));
    }

    public static void main (String [] args) {
        int x = Integer.parseInt(args[0]);
        int y = Integer.parseInt(args[1]);
        System.out.println("a(" + x + "," + y + ") = " + ackermann(x,y));
    }
}

Für die Zahlen $2$ und $11$ erhalten wir beispielsweise (rechne nach...):

alfred@duron:~/java/themen> java Ackermann 2 11
a(2,11) = 25