Die Hofstaedter-Funktion

Die Hofstaedter-Funktion ist folgendermaßen rekursiv definiert:

$$\begin{eqnarray*} \lefteqn{ h_1=1 } \\ \lefteqn{h_2=1} \\ \lefteqn{h_n = h_{n-h_{n-1}} + h_{n-h_{n-2}}} \end{eqnarray*}$$

Schwierig? Wir berechnen die ersten Werte:

$$\begin{eqnarray*} \lefteqn{h_1=1} \\ \lefteqn{h_2=1} \\ \lefteqn{h_3=h_{3-2} +... ...{h_7=h_{7-4} + h_{7-3} = h_3 + h_4 = 2+3 = 5} \\ \lefteqn{...} \end{eqnarray*}$$

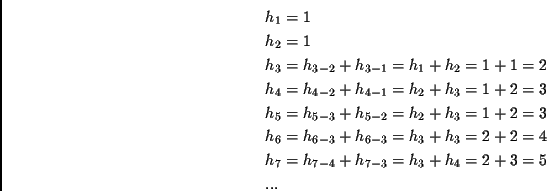
public class Hofstaedter {
    


    public static void main (String [] args) {
        int maxzahl;
        maxzahl = Integer.parseInt(args[0]);
        int [] hof = new int [maxzahl+1];
        hof[1]=1;
        hof[2]=1;
        System.out.println("1: " + hof[1]);
        System.out.println("2: " + hof[2]);
        for (int i=3; i<=maxzahl; i++) {
            hof[i]=hof[i-hof[i-1]] + hof[i-hof[i-2]];
            System.out.println(i + ": " + hof[i]);
        }
    }
}

Die Hofstaedter-Funktion liefert dabei folgende erste 10 Zahlen:

alfred@duron:~/java/themen> java Hofstaedter 10
1: 1
2: 1
3: 2
4: 3
5: 3
6: 4
7: 5
8: 5
9: 6
10: 6

Interessanterweise liefert die Funktion für große Zahlen einen Wert, der etwa dem halben Index entspricht:

100000: 48157