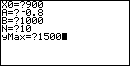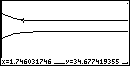Einfache Differenzengleichungen
Wir behandeln Rekursionsgleichungen der Form
x(n+1) = a.x(n) + b; x0
Eine derartige Gleichung heißt lineare Differenzengleichun 1. Ordnung mit dem
Startwert (der Anfangsbedingung) x0. Die Namensgebung erklärt sich aus der folgenden
Umformung:
x(n+1) - x(n) = (a-1).x(n) + b
Man sieht: Die Differenz x(n+1) - x(n) ist eine lineare Funktion von x(n).
Mit einem programmierbaren Taschenrechner lassen sich solche Funktionen schnell darstellen. Wir
verwenden dazu etwa das folgende Programm:
:ClLCD
:AxesOn
:ClDrw
:Prompt X0, A, B, N, yMax
:0->xMin
:N->xMax
:0->yMin
:X0->XS
:For(X,1,N)
:XS->X0
:A*X0+B->XS
:Line(X-1,X0,X,XS)
:End
|

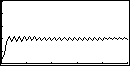
Für diese Werte der Startbedingung x0, der Koeffizienten a und b, sowie die Anzahl n der
Iterationen und dem Wert yMax für die Darstellung erhalten wir den unten dargestellten
Funktionsgraphen.
|
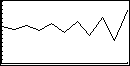
Wir erkennen: Die Werte entfernen sich vom Startwert ("repulsive Funktion").
|
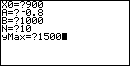
Für andere Eingaben erhalten eine Funktion, deren Werte einem Grenzwert zustreben...
|
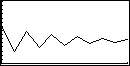
Der Grenzwert wird "Attraktor" genannt
|
Systeme von Differenzengleichungen
Diese treten bei komplexeren Problemen auf. Geht es darum, das Langzeitverhalten zweier Variable zu
beschreiben, muss man ein System von zwei Gleichungen anschreiben:
x(n+1) = ax.x(n) + bx.y(n); x0
y(n+1) = ay.x(n) + by.y(n); y0
Die Koeffizienten ax, bx, ay und by sind in diesem Fall konstant.
Auch für diesen Fall kann ein (kurzes) TI-85 Programm angegeben werden:
:ClLCD
:ClDrw
:AxesOn
:0->xMin
:0->yMin
:Prompt X0,Y0,AX,BX,AY,BY,N,yMax
:N->xMax
:X0->XS
:Y0->YS
:For(X,1,N)
:XS->X0
:YS->Y0
:AX*X0+BX*Y0->XS
:AY*X0+BY*Y0->YS
:Line(X-1,X0,X,XS)
:Line(X-1,Y0,X,YS)
:End
|
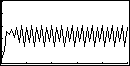
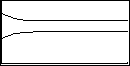
Für die Startwerte x0=20 und y0=40 erhalten wir für das System
x(n+1) = 0,6.x(n) + 0,3.y(n)
y(n+1) = 0,4.x(n) + 0,7.y(n)
folgende Ergebnisse:
|
An Hand der Funktionsgraphen kann das Langzeitverhalten des Systems leicht abgelesen werden
|
Möchte man Zahlenwerte erhalten, verwendet man die Pfeiltasten im Graphik-Modus
(<TRACE>).
|
 |
 |
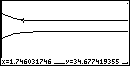 |
Komplizierte Fragestellungen (etwa Wachstumsprozesse) können beispielsweise durch das
"Verhulst-Modell" beschrieben werden.
Die Wachstumsfunktion x(t+1) = k.x(t)
Wir betrachten die Vermehrung einer Tierpopulation: Die Zahl der Tiere im Jahr t+1 ist der Zahl der
Tiere des Vorjahres t proportional. Damit lässt sich sich folgende exponentielle Gleichung angeben:
k ... Vermehrungsrate (hängt z.B. vom Nahrungsangebot ab)
x(0) ... Zahl der Tiere zu Beginn
x(1) ... Zahl der Tiere nach einem Jahr
x(t) ... Zahl der Tiere zum Zeitpunkt t
x(t+1) = k.x(t)
x(1) = k.x(0)
x(2) = k.x(1) = k.k.x(0) = k².x(0)
x(3) = k.x(2) = k.k².x(0) = k³.x(0)
...
x(t) = k^n.x(0)
Ein solcher exponentieller Zusammenhang lässt sich für zahlreiche Wachstums- oder
Zerfallsprozesse (z.B. radioaktiver Zerfall) angeben. Ein exponentielles Anwachsen der Tierpopulation ist
aber nur bei beliebig viel Nahrungsangebot und beliebig viel Platz möglich. Da dies in der Natur nicht
zutrifft, muss für obige Gleichung ein Korrekturterm mit negativem Vorzeichen berücksichtigt
werden, der die Tierpopulation im Folgejahr verringert:
Logistische Gleichung (Verhulst-Dynamik)
k ... Vermehrungsrate
r ... Reduktionsrate (Krankheitsepidemien, Nahrungsmangel, ...)
x(t) ... Zahl der Tiere zum Zeitpunkt t
x(t+1) ... Zahl der Tiere zum darauffolgenden Zeitpunkt t+1
Wir erhalten die Gleichung x(t+1) = k.x(t) - r.x(t)²
Ist die Zahl der Tiere x(t) klein, so ist der Korrekturterm -r.x(t)² so klein, dass
er weggelassen werden kann. Die Zunahme der Tiere erfolgt dann exponentiell. Bei großer Zahl der Tiere
führt der Korrekturterm zu einer Abnahme der Tiere (z.B. Seuchen).
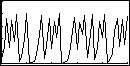
Wir verwenden das zugehörige Programm lwt.85p mit dem TI-85:
Wir erkennen, dass mit steigendem Wert für k die Zahl der
"Grenzwerte" zunimmt. Ab bestimmten Werten von k verdoppelt sich die Zahl
der Grenzwerte ("Periodenverdopplung"). Diese Periodenverdopplung
lässt sich im sogenannten Bifurktionsdiagramm darstellen. Das
folgende Programm bif.85p berechnet dieses
Diagramm...
Bifurkationsdiagramm
Die logistische Gleichung kann in der Form f(x) = a.x.(1-x)
geschrieben werden, wobei a einen Wert zwischen 1 und 4 annimmt. Diese
Funktionsgleichung wird zunächst mit dem [GRAPH]-Menü als
Funktion y1 eingetragen:
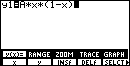
Zu beachten ist auf jeden Fall, dass die Funktion zur graphischen
Darstellung nicht selektiert ist.
Wir untersuchen das Verhalten jedes dynamischen Systems, das zu
einem bestimmten Wert von A gehört. Dazu lassen wir A in einem
Bereich von 2.95 und 4 variieren und berechnen jeweils die Zahl und die
"Lage" der zugehörigen Grenzwerte in Abhängigkeit von A. Wie aus
den Abbildungen der Kurven zur logistischen
Gleichung ersichtlich ist, treten diese Grenzwerte nach einer mehr
oder weniger langen "Einschwingzeit" auf - sie ist im unten
angeführten Programm mit 100 Iterationen festgelegt.
PROGRAM:BIF
:0->xMin Abmessungen des Grafikfensters
:126->xMax
:0->yMin
:62->yMax
:AxesOff
:ClDrw
:For(XS,0,126) Jeden Punkt ausnützen
:2.95+XS/120->A Den Wert für A berechnen
:.01->XR Anfangswert wählen
:For(I,1,100) Einschwingzeit
:evalF(y1,x,XR)->XR
:End
:For(I,1,40) 40 Iterationen
:evalF(y1,x,XR)->YR
:round((1-YR))*62->YS
:PtOn(XS,YS)
:YR->XR
:End
:End
|
|
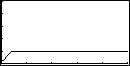
Wir erhalten damit das folgende Bifurkationsdiagramm:
|
 |
 |
 |
| |
Da die Rechenzeit am TI-85 eine gute
halbe Stunde
beträgt, empfiehlt es sich, das fertige Bild abzuspeichern:
[GRAPH]-[MORE]-[MORE]-<STPIC> |
Obwohl jedes Bild aus 127x63
Bildpunkten
zusammengesetzt ist, benötigt es "nur" 1020 Bytes Speicher
(darüber erhält man im [MEM]-Menü Auskuft |