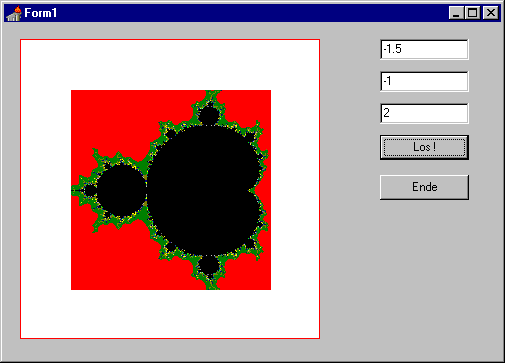
... wird auch "Apfelmännchen" - wegen seiner charakteristischen Form - genannt ;-). Wie auch immer: Das Gebilde ist ein Fraktal, das durch eine rekursive definierte Folge von komplexen Zahlen entsteht.
z(n+1) = z(n)²+c
Stellen wir die komplexe Zahl z mit Realteil x und Imaginärteil y dar, und sind a und b Real- und Imaginärteil der Zahl c so erhalten wir:
(x,y) := (x² - y²,2*x*y) + (a,b)
Konvergiert ein Punkt der komplexen Zahlenebene bei der angegebenen Rekursion, so ist er ein Element der sogenannten Mandelbrot-Menge (genannt nach dem Mathematiker B.B. Mandelbrot, der diese Beziehungen in der 2. Hälfte des 20. Jahrhunderts untersuchte). Strebt ein Punkt gegen Unendlich, so wird er "verworfen" und der nächste Punkt wird untersucht...
Diese Gleichung lösen wir koordinatenweise auf und codieren eine entsprechende Iteration über alle Punkte eines gewählten Quadrates der komplexen Zahlenebene. Das Quadrat wird durch den "Eckpunkt" (amin, bmin) und durch seine Kantenlänge k festgelegt. Zusätzlich müssen die Punkte der komplexen Zahlenebene auf ein Bildschirmquadrat (im untenstehenden Programm 200x200 Pixel) "gezoomt" werden. Dazu dividieren wir die Kantenlänge des Quadrats durch 200 (Zahl der Pixel, Schrittweite ds:=k/200)und erhöhen bei jeder Iteration den Realteil bzw. den Imaginärteil der komlexen Zahl um diese Schrittweite ds:
var amin,bmin,kante,ds:real;
a,b,x,y,xx,yy:real;
s,z,zaehler:integer;
begin
paintbox1.canvas.brush.color:=clWhite;
paintbox1.canvas.pen.color:=clRed;
paintbox1.canvas.rectangle(0,0,300,300);
amin:=strtoFloat(edit1.text);
bmin:=strtoFloat(edit2.text);
kante:=strtoFloat(edit3.text);
ds:=kante/200;
a:=amin;
for s:=1 to 200 do begin
b:=bmin;
for z:=1 to 200 do begin
x:=0;
y:=0;
zaehler:=0;
while (zaehler<100) and (sqrt(x*x+y*y)<2) do begin
inc(zaehler);
xx:=x*x-y*y+a;
y:=2*x*y+b;
x:=xx;
end;
if zaehler>=100 then paintbox1.canvas.Pixels[s+50,z+50]:=clBlack;
case zaehler of
0..9:paintbox1.canvas.Pixels[s+50,z+50]:=clRed;
10..19:paintbox1.canvas.Pixels[s+50,z+50]:=clGreen;
20..29:paintbox1.canvas.Pixels[s+50,z+50]:=clOlive;
30..39:paintbox1.canvas.Pixels[s+50,z+50]:=clNavy;
40..49:paintbox1.canvas.Pixels[s+50,z+50]:=clYellow;
50..59:paintbox1.canvas.Pixels[s+50,z+50]:=clTeal;
60..69:paintbox1.canvas.Pixels[s+50,z+50]:=clGray;
70..79:paintbox1.canvas.Pixels[s+50,z+50]:=clSilver;
80..89:paintbox1.canvas.Pixels[s+50,z+50]:=clAqua;
90..99:paintbox1.canvas.Pixels[s+50,z+50]:=clLime;
end;
b:=b+ds;
end;
a:=a+ds;
end;
end;
Ein Punkt gehört zur Mandelbrotmenge, wenn er bei der Rekursion nicht gegen unendlich strebt. Im Programm gehen wir davon aus, dass der Punkt bei 100 Iterationen den Kreis mit Radius 2 noch nicht verlassen hat
Gehört ein Punkt zur Mandelbrotmenge, so wird er schwarz "eingefärbt": mit Delphi ist es möglich, den Punkt im Array "Pixels" direkt zu setzen...
"Verlässt" ein Punkt bereits nach weniger als 100 Iterationen den Kreis mit Radius 2 LE, so wird er mit einer anderen Farbe dargestellt - diese Punkte liegen in der Umgebung der (schwarzen) Mandelbrotmenge.